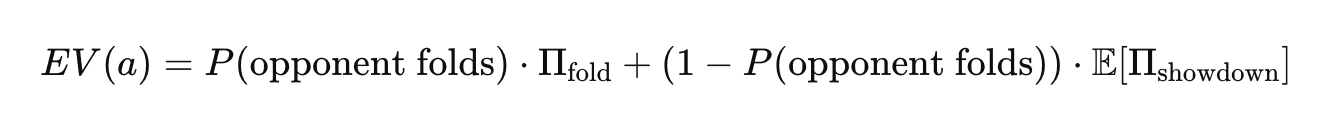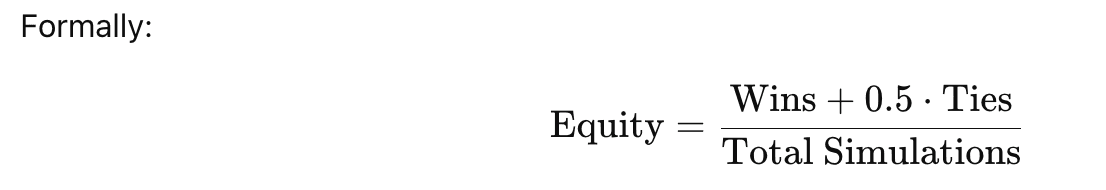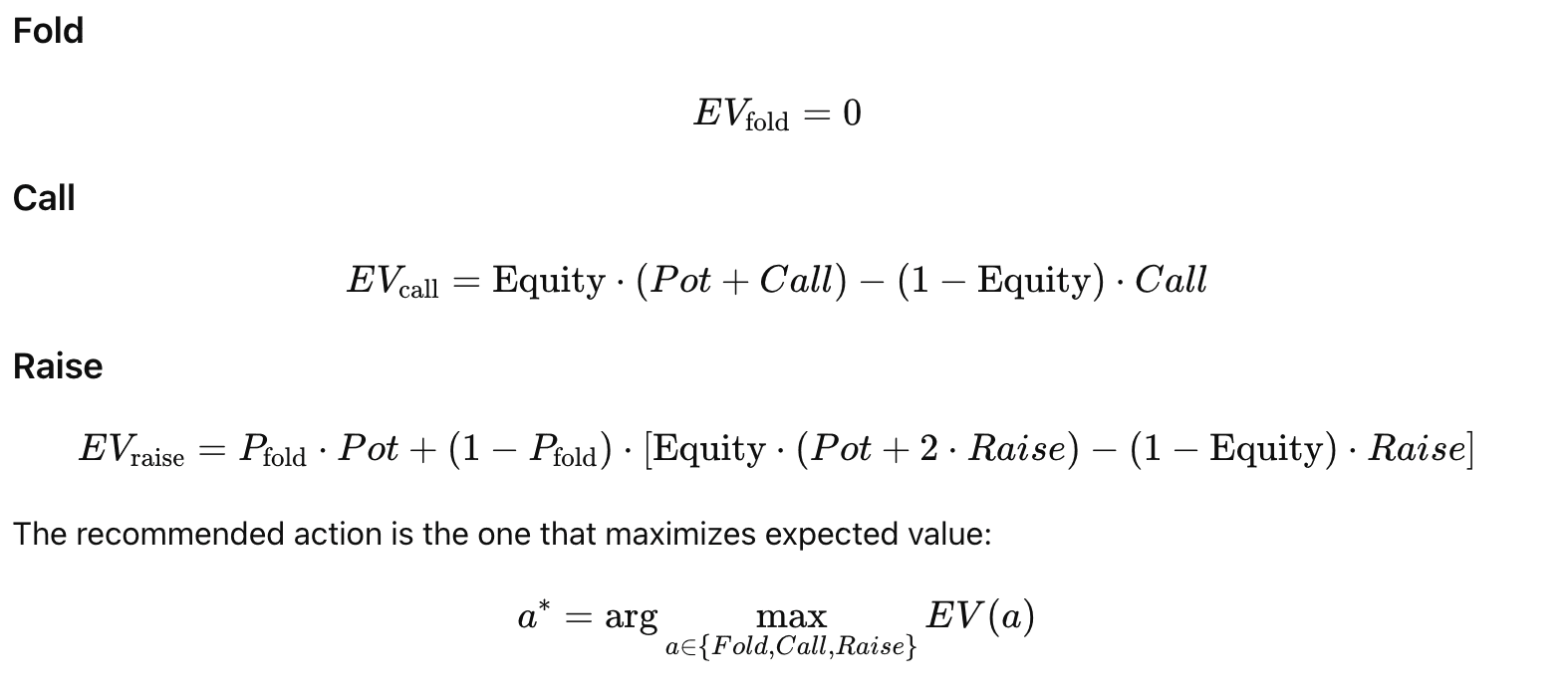Poker Decision Assistant
Model Framework
This project implements a decision-theoretic framework for Heads-Up No-Limit Texas Hold’em, modeling strategic action selection under uncertainty. Unlike deterministic games, poker is an imperfect-information environment, meaning players must make decisions without observing their opponent’s private information.
At each decision point, the application computes expected value (EV) across available actions:
Rather than relying on precomputed lookup tables, the model dynamically samples opponent hands and future board runouts using stochastic simulation. This allows EV estimates to adapt to changing board textures, stack sizes, and opponent tendencies.
Equity Estimation
Equity is estimated using Monte Carlo simulation powered by combinatorial sampling of unseen cards. For each trial:
Known cards (hero hole cards + board) are removed from the deck
Opponent hole cards are sampled from the remaining deck
Remaining community cards are drawn
Hand strength is evaluated using a rank-based evaluator
Outcomes are aggregated over thousands of trials
This stochastic approach mirrors methods used in quantitative finance for pricing under uncertainty, where closed-form solutions are unavailable.
Expected Value Optimization
For each available action (Fold, Call, Raise), the model computes:
This structure mirrors optimal stopping and capital allocation problems in finance, where decision quality is measured by expected payoff rather than realized outcome.
Opponent Modeling
Rather than assuming a static adversary, the model incorporates simplified behavioral parameters:
Fold-to-raise probability
Preflop looseness
Postflop aggression
These inputs influence fold equity and risk–reward trade-offs. While intentionally simplified for interpretability, this structure reflects the core idea of Bayesian belief updating: decisions depend on posterior beliefs about opponent strategy.
Future extensions include weighted range sampling and adaptive belief updating based on observed action frequencies.
Risk & Performance Analytics
Beyond single-hand optimization, the application tracks:
Realized PnL
Expected value per hand
Bankroll trajectory
Maximum drawdown
This transforms the model from a one-shot calculator into a capital allocation simulator. Variance, drawdowns, and EV drift mirror performance dynamics seen in systematic trading strategies.
Interpretation Philosophy
A central design principle of the project is economic interpretability.
The model does not attempt to “predict cards.” Instead, it formalizes decision quality as:
This distinction parallels financial markets:
A trade can be correct in expectation but lose money ex post
A suboptimal decision can appear successful due to variance
By separating EV from realized results, the framework emphasizes process over outcome — a core principle in both game theory and quantitative finance.
Academic Inspiration
This project draws inspiration from foundational work in game theory, stochastic simulation, and decision theory:
Nash, J. (1950)
Equilibrium Points in N-Person Games
Proceedings of the National Academy of Sciences
Von Neumann, J., & Morgenstern, O. (1944)
Theory of Games and Economic Behavior
Billings, D. et al. (2003)
Approximating Game-Theoretic Optimal Strategies for Full-Scale Poker
Brown, N., & Sandholm, T. (2019)
Superhuman AI for Multiplayer Poker
Science
Hull, J. (2018)
Options, Futures, and Other Derivatives
These works motivate the project’s emphasis on equilibrium reasoning, stochastic modeling, and expected-value maximization in uncertain environments.